The entanglement properties of qubits used in quantum computing are exploited. However, the state vector of qubits need not be entangled.
A composite system is formed by the tensor product of the sub-physical systems that compose it.
Let's consider two systems, A and B.
If there is a correlation between these A and B systems, we can write the tensor product of these systems as follows.
However, if there is no correlation between systems A and B, these systems are entangled and the above equation cannot be written.
For example,
Question: Can we write as |ψ> = |A>|B>?
The answer is no, we cannot write this equation. because,
The answer is no, we cannot write this equation. because,
However, we can write the tensor product expression in its most general form, whether it is entangled or not.




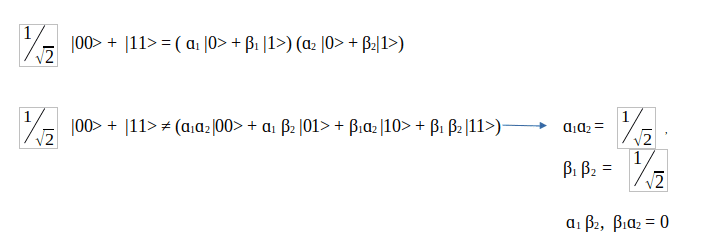


Very good comment.
ReplyDelete