Proof of Cauchy–Schwartz Inequality

The Cauchy-Schwartz inequality is one of the important geometric properties of Hilbert space. The proof of this inequality is as follows:

First, let's examine the left-hand side of the inequality.

Let us now consider the right-hand side of the inequality. We can write the unit operator, which is the sum of all orthonormal basis kets in the Hilbert space.

Let's look at an example that satisfies this inequality.

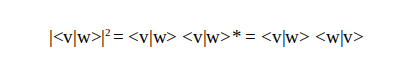
Comments

Bloch Sphere – Geometric Representation of Quantum State

It is very difficult to visualize quantum states before our eyes. The Bloch sphere represents quantum state functions quite well. The Bloch sphere is named after physicist Felix Bloch. As you can see in the Bloch sphere figure below, it geometrically shows the pure states of two-level quantum mechanical systems. The poles of the Bloch sphere consist of bits |0⟩ and |1⟩. Classically, the point on the sphere indicates either 0 or 1. However, from a quantum mechanics point of view, quantum bits contain possibilities to be found on the entire surface of the sphere. Traditionally, the z-axis represents the |0⟩ qubit, and the z-axis the |1⟩ qubit. When the wave function in superposition is measured, the state function collapses to one of the two poles no matter where it is on the sphere. The probability of collapsing into either pole depends on which pole the vector representing the qubit is closest to. The angle θ that the vector makes with the z-axis determines this probabilit...

Bernstein–Vazirani Algorithm

Quantum computers currently available are not sufficient to solve every existing classical problem due to their own characteristics. This does not mean that they are inferior to classical computers, or that, on the contrary, quantum computers should give all kinds of advantages over classical computers. Popular quantum algorithms solved in quantum computers are algorithms created by taking advantage of the superposition and entanglement properties of particles. So, they are algorithms created to show the prominent features of quantum properties. Today I will talk about an enjoyable algorithm that demonstrates the efficiency and speed of these quantum features. Known as the Bernstein - Vazirani algorithm is a quantum algorithm invented by Ethan Bernstein and Umesh Vazirani in 1992. The purpose of this algorithm, which is a game, is to find a desired number. To put it more clearly, let's keep in mind a string of binary numbers, for example, 1011001. Next, let's write an algori...

Shor's Protocol - Example Solution

Finally, we have come to the famous Shor's definition of the algorithm in this article. Before applying this algorithm, we examined in detail the three mathematical operations required for our algorithm. These three necessary mathematical expressions were modular arithmetics, quantum Fourier transform , and quantum phase estimation . As you may remember, Shor's algorithm is an algorithm that gives prime factor values of large numbers. To show that this protocol works, we will write an algorithm that gives the prime factors of 15. The binary equivalent of the decimal number 15 consists of 1111 qubits. Now let's examine Shor's protocol in detail. If we write it in a regular way, we can write the state vector | ψ 3 > as follows. Now, let's measure the last four qubits. In this case, we would have measured the situations |1>, |2>, |4>, |8> with 25% probability. Suppose we have reached the state |8> with a probability of 25% in our measurement re...

Era Quantic | Quantum Computing and Information Articles

Search This Blog