Quantum Superdense Coding Protocol

One of the most basic applications of quantum algorithms is superdense coding. It is a simple protocol, but it is also an important protocol. Now let's take a detailed look.

The setup of the protocol is as follows:

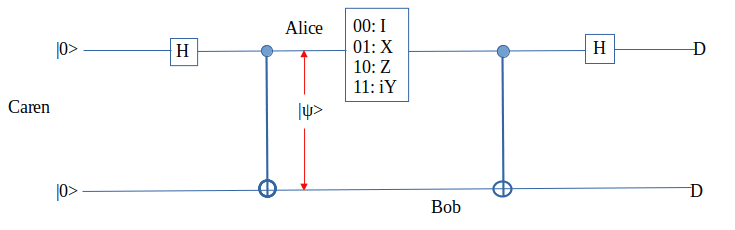
Alice wants to send 2-qubit information to Bob, but she can only send a single-qubit due to her possibilities. But how does Bob get a 2-qubit of information from Alice?

This is where Caren comes in. Caren entanglements 2 qubits through Hadamard and CNOT. It sends one of the entangled particles to Alice and the other to Bob. Alice and Bob have no information as they do not measure which particle has come to them.

From here on, Alice will be able to send the qubits she wants to Bob. Let's examine them all in turn.

Let Alice wants to send the 00 qubits. In this case, it will use the I gate.

Let Alice wants to send the 01 qubits. In this case, it will use the X gate.

Let Alice wants to send the 10 qubits. In this case, it will use the Z gate.

Let Alice wants to send the 11 qubits. In this case, it will use the iY gate.

As can be seen, Bob finds the qubit information sent by Alice in the measurement results with 100% probability.

Let's focus on the important point above. For this protocol to work correctly, the qubits to be created must be entangled. Otherwise, if they are not entangled, Bob will get different results with different probabilities.

The entangled states you see above are called Bell States. As I mentioned before, in order to obtain an accurate measurement result with a 100% probability of the quantum superdense coding protocol, it is necessary to start the process with one of the Bell entanglement states.

I will write about different protocols in my future articles.

Stay with physics. :)

Reference

https://www.youtube.com/watch?v=3wCW4x51Blo&list=PLqNc_xpYGu77u6dI_RijjCLd-nP8p_4pI&index=22

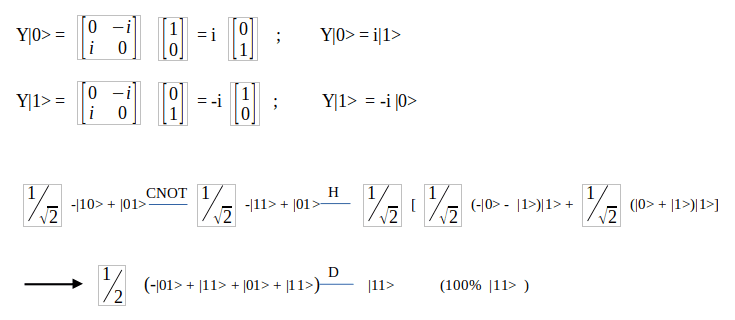
Comments

Statement of Bell's Inequality

One of the most important applications of quantum mechanics is Bell's inequality. In 1965, John Stewart Bell actually thought that Einstein might be right and tried to prove it, but proved that quantum logic violated classical logic. It was a revolutionary discovery. Let's look at its mathematically simple explanation. To create the analogy, let's first write a classical inequality. This inequality above is a classic expression. The quantum analogy of this expression represents the Bell inequality. With just one difference. Bell's inequality shows that the above equation is violated. Expressing Bell's inequality by skipping some complicated mathematical intermediates; While there is no such situation in the classical world that will violate the inequality we mentioned at the beginning, it is difficult to find a situation that does not violate this inequality in the quantum world. Reference https://www.youtube.com/watch?v=lMyWl6Pq904 https://slideplay...

Bloch Sphere – Geometric Representation of Quantum State

It is very difficult to visualize quantum states before our eyes. The Bloch sphere represents quantum state functions quite well. The Bloch sphere is named after physicist Felix Bloch. As you can see in the Bloch sphere figure below, it geometrically shows the pure states of two-level quantum mechanical systems. The poles of the Bloch sphere consist of bits |0⟩ and |1⟩. Classically, the point on the sphere indicates either 0 or 1. However, from a quantum mechanics point of view, quantum bits contain possibilities to be found on the entire surface of the sphere. Traditionally, the z-axis represents the |0⟩ qubit, and the z-axis the |1⟩ qubit. When the wave function in superposition is measured, the state function collapses to one of the two poles no matter where it is on the sphere. The probability of collapsing into either pole depends on which pole the vector representing the qubit is closest to. The angle θ that the vector makes with the z-axis determines this probabilit...

Let's Define Quantum Programming

Along with the strange discoveries of quantum physics, one of these ideas for how we could use it is quantum computers. Work on quantum computers, which is a pretty good idea, started small and became what it is today. Now we had to take one more step and do quantum programming. The first studies on this process were made in the early 2000s. However, these studies were more theoretical. This was because quantum computers were not yet technologically ready. Finally, with the serious development of quantum computers (of course, we are still not at the desired point) we started to create our quantum algorithms. Today, we can do these algorithms on IBM Quantum Experience, Microsoft Azure Quantum, DWave Leap Cloud, or with quantum development kits. With these platforms, most of which are open source, we can create our quantum algorithms with the Python language, which we use classically and which is the most common programming language. The fact that such platforms are open sou...

Era Quantic | Quantum Computing and Information Articles

Search This Blog